概要
最近数学を学び直した際、積分で面積が求まる理由が曖昧だった為、自分用の備忘録。
微分
まず積分で面積を求める前に前提としての「微分」についてから。
「微分」とは瞬間的な傾きを求めること。
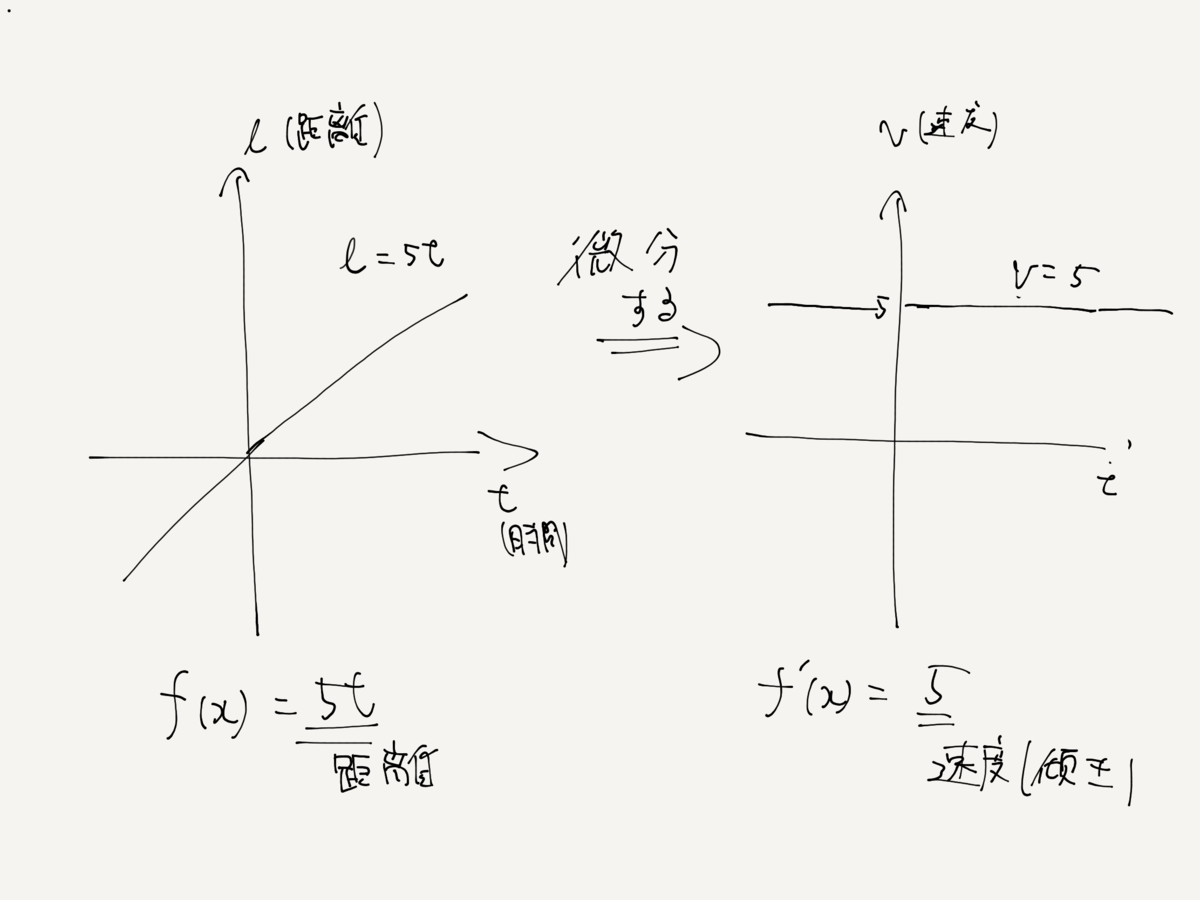
例えば、ある時間の「距離」を微分すると、その時の「速度(傾き)」を求めることができる。
積分で面積を求める
本題。
まず単純に面積を求めようとすると
「底辺」× 「 高さ」
で求めることができる。
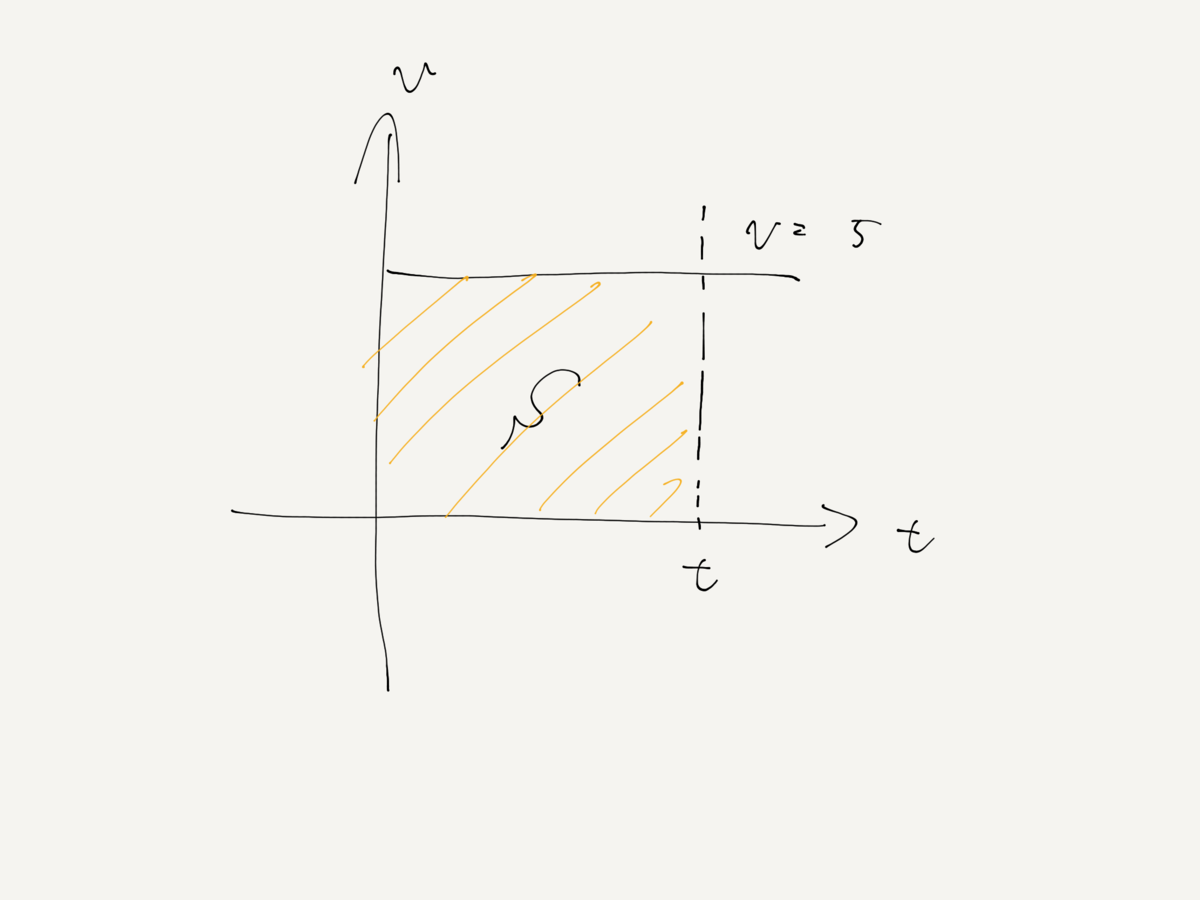
そして下記画像のような時間と速度を表したグラフにおいて範囲内の面積を求めるということは、
「時間」× 「 速度」で「距離」を求めることになる。
そして上記のグラフ面積を求める式は
と表される。
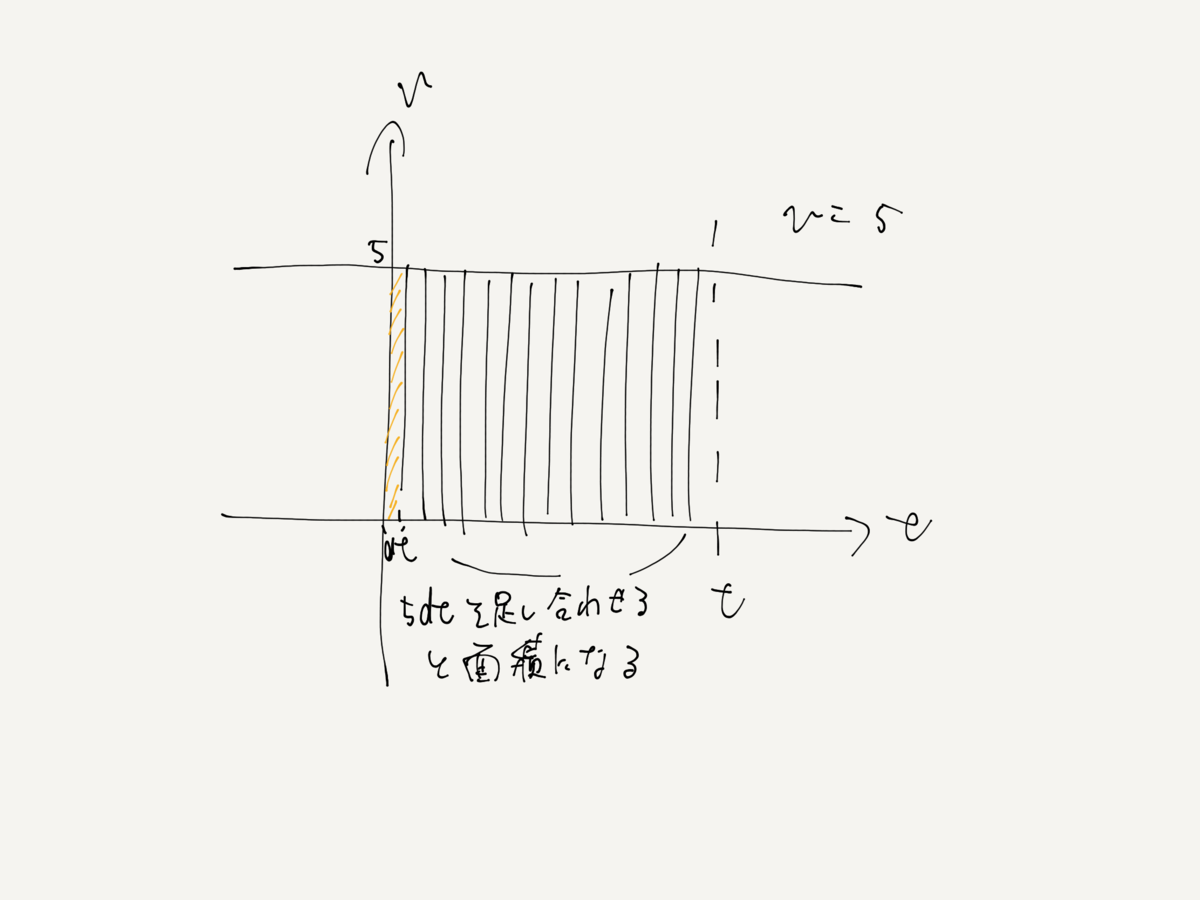
面積は「底辺」×「高さ」だけではなく、 細分化した面積を足し合わせるという方法でも求めることができる。
この時、底辺である時間を極限まで小さくし、これを「dt」とする。
このとき上記グラフの0からtまでの間の面積を求めようとすると、
5(速度)*dt(距離) をt個足して合わせると面積になる。
この時の速度である5は、距離から微分することができる。 よって、微分した結果をもとの関数に戻す(積分)により面積を求めることができる。
